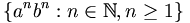Turing machine simulator (Scheme)

From LiteratePrograms

We describe a simple Scheme program for simulating an abstract Turing machine. This demonstrates that Scheme is Turing-complete (with the caveat that limitations in word size limit the effective addressable memory).

Formal problem description and assumptions

We define a single-tape Turing machine as a 6-tuple 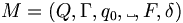$M=(Q, \Gamma, q_0, \textvisiblespace, F, \delta)$ , where

$Q$ is a finite set of states;
$Γ$ is the finite tape alphabet (the symbols that can occur on the tape);
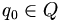$q_0 \in Q$ is the initial state;
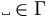$\textvisiblespace \in \Gamma$ is the blank symbol;
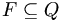$F \subseteq Q$ is the set of accepting (final) states;
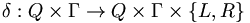$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ is the transition function which determines the action performed at each step.

Initially the tape has the input string on it, followed by an infinite number of blank symbols ( $\textvisiblespace$ ), and the head is at the left end of the tape. At each step we use the transition function to determine the next state, the symbol written on the tape just prior to moving, and the direction to move the head, left (L) or right (R). If we ever reach a final state, the machine halts.

Main simulator

State representation

We will represent the tape by a list of Scheme symbols. States are encoded as integers, the symbol invalid marks the invalid state.

Simulation

The main function of our simulator is simulate which performs a single execution step. The first three parameters represent the current execution state, the remainder describes the Turing machine and remains constant throughout the calculation. simulate shall return #t if the machine halts on an accepting state and #f if it reaches an invalid state.

<<simulator>>=
(define (simulate tape state head-position transition-func accepting-states blank-symbol)
  trace current state
  act according to current state)

In a single simulation step, we have three possible cases depending on the current state value:

<<act according to current state>>=
(cond (machine in invalid state)
      (machine in accepting state)
      (else machine running))

In invalid state, the machine stops and returns #f.

<<machine in invalid state>>=
(eq? state 'invalid) #f

Likewise, if the current state is in the set of accepting states, we stop and return #t.

<<machine in accepting state>>=
(member state accepting-states) #t

As long as we're neither in invalid or accepting state, we read the symbol at the current tape position and call the transition function to determine new state, the symbol to write to the tape, and the head move direction:

<<machine running>>=
(let ((symbol read symbol at current head position))
  (let-values (((newstate newsymbol movedir) (transition-func state symbol)))
    next simulation step))

To read a symbol from the tape, we define a small utility function that takes a few special cases into account.

<<utility functions>>=
(define (symbol-at tape position blank-symbol)
  (cond ((< position 0)              (error "Invalid tape position"))
        ((>= position (length tape)) blank-symbol)
        (else                        (list-ref tape position))))

With its help, reading the current symbol from the tape is straightforward:

<<read symbol at current head position>>=
(symbol-at tape head-position blank-symbol)

For the next simulation step, we call simulate recursively with an updated tape and head position.

<<next simulation step>>=
(simulate update tape
          newstate
          determine new head position
          transition-func
          accepting-states
          blank-symbol)

The head position is updated according to the symbol in movedir.

<<determine new head position>>=
(cond ((eq? movedir 'left)  (- head-position 1))
      ((eq? movedir 'right) (+ head-position 1))
      (else (error "Illegal head move")))

Before the next step, we write the symbol returned by the transition function to the old head position.

<<update tape>>=
(write-to-tape tape head-position newsymbol)

This is done by another utility function write-to-tape we define as follows:

<<utility functions>>=
(define (write-to-tape tape position symbol)
  (let ((l (length tape)))
    (cond ((or (< position 0)
               (> position l))  (error "Invalid tape position"))
          ((= position l)       (append tape (list symbol)))
          (else                 replace symbol on tape))))

If the symbol is in the middle of the tape, we copy the tape up to the current position and append the new symbol and the rest of the tape.

<<replace symbol on tape>>=
(replace-symbol tape position symbol)

<<utility functions>>=
(define (replace-symbol tape position symbol)
  (letrec ((replace-helper (lambda (tape n acc)
                             (if (= n 0)
                               (append (reverse acc) (cons symbol (cdr tape)))
                               (replace-helper (cdr tape) (- n 1) (cons (car tape) acc))))))
    (replace-helper tape position '())))

Tracing State

For diagnostic purposes, it's also useful to print out some of the details of a state. We only show the first trace-tape-chars characters of the tape:

<<constants>>=
(define trace-tape-chars 78)
<<trace current state>>=
(trace-state tape head-position blank-symbol)
<<utility functions>>=
(define (trace-state tape head-position blank-symbol)
  (letrec ((print-n-times (lambda (s n)
                            (when (> n 0)
                              (display s)
                              (print-n-times s (- n 1)))))
           (print-tape (lambda (tape n)
                         (when (not (or (null? tape)
                                        (= n 0)))
                           (display (car tape))
                           (print-tape (cdr tape) (- n 1))))))
    (when (< head-position trace-tape-chars)
      (print-n-times #\space head-position)
      (display "v\n"))
    (print-tape tape trace-tape-chars)
    (print-n-times blank-symbol (max 0 (- trace-tape-chars (length tape))))
    (display "\n")))

Files

Finally, we put it all together into a source file:

<<simulate_turing_machine.scm>>=
constants
utility functions
simulator

This completes the simulator implementation.

Test driver

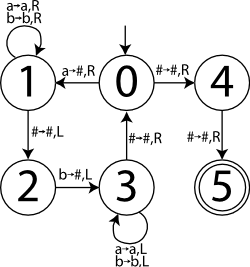
A simple Turing machine recognizing the language aⁿbⁿ

To test the simulation, we'll implement the simple Turing machine shown to the right, which is based roughly on this Turing machine example. This diagram is a state graph, meaning that each vertex represents a state in the machine's finite control, and each edge indicates the input character that must be read to follow that edge, the character to write over it, and the direction to move the head. The initial state is 0 and the only accepting state is 5. It recognizes the following context-free but nonregular language:

$\{{a^n}{b^n} : n \in \mathbb{N}, n \geq 1\}$

The pumping lemma says that this is nonregular, but a Turing machine to recognize it is fairly straightforward. The main task is to transform the state graph into a transition function. We could code such a function for each program we run on the simulator, but a much better idea is to write a generic function which reads the appropriate return values from a data table.

To keep it simple, we use a data table of list of lists that each hold an input and its corresponding output values. For inputs that do not match any entry in the table, the invalid state is returned.

<<utility functions>>=
(define (find-trans-state states state symbol blank-symbol)
  (if (null? states)
    (values 'invalid blank-symbol 'left)
    (if (equal? (list state symbol) (caar states))
      (let ((s (cadar states)))
        (values (list-ref s 0) (list-ref s 1) (list-ref s 2)))
      (find-trans-state (cdr states) state symbol blank-symbol))))

Now we're ready to define our aⁿbⁿ test. We pick # for the blank symbol.

<<test_driver.scm>>=
(define test-states
  '(((0 \#) (4 \# right))
    ((0 a)  (1 \# right))
    ((4 \#) (5 \# right))
    ((1 a)  (1 a  right))
    ((1 b)  (1 b  right))
    ((1 \#) (2 \# left))
    ((2 b)  (3 \# left))
    ((3 a)  (3 a  left))
    ((3 b)  (3 b  left))
    ((3 \#) (0 \# right))))
(define (test-anbn-trans-func state symbol)
  (find-trans-state test-states state symbol '\#))
(define (anbn-test initial-tape)
  (simulate initial-tape 0 0 test-anbn-trans-func '(5) '\#))

Now we can see, for example:

<<example_output.txt>>=
> (anbn-test '(a b))
v
ab############################################################################
 v
#b############################################################################
  v
#b############################################################################
 v
#b############################################################################
v
##############################################################################
 v
##############################################################################
  v
##############################################################################
   v
##############################################################################
#t

See Turing machine simulator (Scheme)/Example output for a longer example output.

Download code

Retrieved from "http://literateprograms.org/Turing_machine_simulator_%28Scheme%29"

Categories: Turing machine simulators | Programming language:Scheme | Environment:Portable