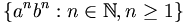Turing machine simulator (Java)

From LiteratePrograms

We describe a simple Java program for simulating an abstract Turing machine. This demonstrates that Java is Turing-complete (with the caveat that limitations in word size limit the effective addressable memory).

Formal problem description and assumptions

We define a single-tape Turing machine as a 6-tuple 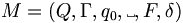$M=(Q, \Gamma, q_0, \textvisiblespace, F, \delta)$ , where

$Q$ is a finite set of states;
$Γ$ is the finite tape alphabet (the symbols that can occur on the tape);
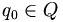$q_0 \in Q$ is the initial state;
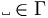$\textvisiblespace \in \Gamma$ is the blank symbol;
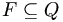$F \subseteq Q$ is the set of accepting (final) states;
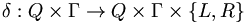$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ is the transition function which determines the action performed at each step.

Initially the tape has the input string on it, followed by an infinite number of blank symbols ( $\textvisiblespace$ ), and the head is at the left end of the tape. At each step we use the transition function to determine the next state, the symbol written on the tape just prior to moving, and the direction to move the head, left (L) or right (R). If we ever reach a final state, the machine halts.

Main simulator

State representation

We allow the alphabet ( $Γ$ ) to be any class type by making all of the classes in our program generic, and take the symbol type as a type variable Symbol.

States ( $Q$ ) of the Turing machine will be represented by a ControlState class:

<<ControlState class>>=
class ControlState<Symbol> {
    public final String name;
    ControlState members
    public String toString() { return name; }
}

This class contains some additional fields that will be described later.

Machine representation

The TuringMachine class contains the initial state ( $q 0$ ) and the blank symbol ( $\textvisiblespace$ ) of the machine.

<<TuringMachine class>>=
class TuringMachine<Symbol>
{
    public final ControlState<Symbol> initialControlState;
    public final Symbol blankSymbol;
    public TuringMachine(ControlState<Symbol> x, Symbol b)
    {
        initialControlState = x; blankSymbol = b;
    }
}

As described above, we use the ControlState class to represent a state. We will add some fields of it to represent some state-specific aspects of the Turing machine. It contains a flag indicating whether the state is an accepting state (whether it is a member of $F$ ), and also a transition mapping indicating what to do given a specific symbol ( $δ$ when applied to this state).

<<imports>>=
import java.util.Map;
import java.util.HashMap;
<<ControlState members>>=
public final boolean accepting;
public final Map<Symbol,TransitionResult<Symbol>> transitions
    = new HashMap<Symbol,TransitionResult<Symbol>>();
public ControlState(String n, boolean a) { name = n; accepting = a; }

The "transitions" field is a Map from Symbol to TransitionResult objects, indexed by the current symbol under the tape head. The TransitionResult object represents the three-tuple range of the transition function used to produce the next state:

<<Transition function result structure>>=
class TransitionResult<Symbol> {
    public final ControlState<Symbol> controlState;
    public final Symbol writeSymbol;
    public final Direction dir;
    public TransitionResult(ControlState<Symbol> c, Symbol s, Direction d)
    {
        controlState = c; writeSymbol = s; dir = d;
    }
}

Simulation representation

We represent the state of the machine at a single instant using the following class, which describes the tape contents, the current control state, and the current position of the head on the tape:

<<imports>>=
import java.util.List;
<<TuringSimulator class>>=
public class TuringSimulator<Symbol> {
    constants
    public final TuringMachine<Symbol> machine;
    public ControlState<Symbol> controlState;
    public int headPosition = 0; // Initially at left end
    public final List<Symbol> tape;
    TuringSimulator constructor
    update method
    trace method
    simulate method
    convenience methods
    main method
}

To initialize the state, we initialize the tape with the input string, position the head at the start of the tape, and set the initial control state:

<<imports>>=
import java.util.ArrayList;
<<TuringSimulator constructor>>=
public TuringSimulator(TuringMachine<Symbol> m, List<Symbol> inputString) {
    machine = m;
    controlState = machine.initialControlState;
    tape = new ArrayList<Symbol>(inputString);
}

We can update this object based on what the transition function tells us to do. It supplies a new control state, a character to write, and a direction in which to move the head:

<<Direction enum>>=
enum Direction { LEFT, RIGHT };
<<update method>>=
public void update(ControlState<Symbol> newControlState, Direction dir, Symbol writeSymbol)
{
    controlState = newControlState;
    if (headPosition < tape.size())
        tape.set(headPosition, writeSymbol);
    else if (headPosition == tape.size())
        tape.add(writeSymbol);
    else
        assert false;
    switch (dir) {
    case LEFT:
        assert headPosition > 0;
        headPosition--;
        break;
    case RIGHT:
        headPosition++;
        break;
    }
}

Note that the head is prevented from moving off the left end. We dynamically expand the tape when the head moves past the right end.

For diagnostic purposes, it's also useful to print out some of the details of a state. We only show the first TRACE_TAPE_CHARS characters of the tape:

<<constants>>=
public static final int TRACE_TAPE_CHARS = 60;
<<trace method>>=
public void trace() {
    for (int i = -17; i < TRACE_TAPE_CHARS; i++) {
        if (i >= headPosition) {
            System.out.print("v"); // points down
            break;
        }
        System.out.print(" ");
    }
    System.out.println();
    System.out.printf("%15s: ", controlState);
    for (int i = 0; i < TRACE_TAPE_CHARS; i++) {
        System.out.print(tapeAt(i));
    }
    System.out.println();
}

Finally, we provide convenience methods to fetch symbols from the tape. The tapeAt method abstracts access to the tape so we see a blank symbol anywhere the tape has not been written to. The currentSymbol method gives us the symbol currently under the head.

<<convenience methods>>=
public Symbol tapeAt(int pos)
{
    return (pos < tape.size()) ? tape.get(pos) : machine.blankSymbol;
}
public Symbol currentSymbol() { return tapeAt(headPosition); }

Simulation

We now come to our primary simulation method. It steps through successive states:

<<simulate method>>=
public void run() {
    trace();
    while (!controlState.accepting) {
        TransitionResult<Symbol> next = controlState.transitions.get(currentSymbol());
        if (next == null) {
            System.out.println("invalid transition");
            break;
        }
        update(next.controlState, next.dir, next.writeSymbol);
        trace();
    }
}

If we run the program on a string in the language, like "aaabbb", the program will return quickly. To ensure it's going through the right intermediate states, we called trace() to print out the states.

If the transition for a specific state and symbol is null (i.e. the transition was not specified), that means the input is not in the language, and we stop.

Files

Finally, we put it all together into a header file and a source file, using the usual idiom to avoid multiple inclusion of the header:

<<TuringSimulator.java>>=
imports
Direction enum
ControlState class
Transition function result structure
TuringMachine class
alphabet
TuringSimulator class

This completes the simulator implementation.

Test driver

First we define our alphabet.

<<alphabet>>=
enum MySymbol
{
    A("a"), B("b"), BLANK("#");
    private final String ch;
    MySymbol(String s) { ch = s; }
    public String toString() { return ch; }
    public static List<MySymbol> parseString(String s)
    {
        List<MySymbol> result = new ArrayList<MySymbol>();
        for (int i = 0; i < s.length(); i++) {
            switch (s.charAt(i)) {
            case 'a': result.add(A); break;
            case 'b': result.add(B); break;
            default: assert false;
            }
        }
        return result;
    }
}

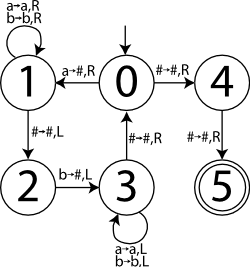
A simple Turing machine recognizing the language aⁿbⁿ

To test the simulation, we'll implement the simple Turing machine shown to the right, which is based roughly on this Turing machine example. This diagram is a state graph, meaning that each vertex represents a state in the machine's finite control, and each edge indicates the input character that must be read to follow that edge, the character to write over it, and the direction to move the head. The initial state is 0 and the only accepting state is 5. It recognizes the following context-free but nonregular language:

$\{{a^n}{b^n} : n \in \mathbb{N}, n \geq 1\}$

The pumping lemma says that this is nonregular, but a Turing machine to recognize it is fairly straightforward. Here's how we construct a Turing machine object for it:

<<initialize example turing machine>>=
initialize states
TuringMachine<MySymbol> machine = new TuringMachine<MySymbol>(s0, MySymbol.BLANK);

We add entries for each arc in the diagram:

<<initialize states>>=
ControlState<MySymbol> s0 = new ControlState<MySymbol>("start", false);
ControlState<MySymbol> s1 = new ControlState<MySymbol>("scan_right", false);
ControlState<MySymbol> s2 = new ControlState<MySymbol>("reverse", false);
ControlState<MySymbol> s3 = new ControlState<MySymbol>("scan_left", false);
ControlState<MySymbol> s4 = new ControlState<MySymbol>("check", false);
ControlState<MySymbol> s5 = new ControlState<MySymbol>("finish", true);
s0.transitions.put(MySymbol.BLANK, new TransitionResult<MySymbol>(s4, MySymbol.BLANK, Direction.RIGHT));
s0.transitions.put(MySymbol.A,     new TransitionResult<MySymbol>(s1, MySymbol.BLANK, Direction.RIGHT));
s4.transitions.put(MySymbol.BLANK, new TransitionResult<MySymbol>(s5, MySymbol.BLANK, Direction.RIGHT));
s1.transitions.put(MySymbol.A,     new TransitionResult<MySymbol>(s1, MySymbol.A,     Direction.RIGHT));
s1.transitions.put(MySymbol.B,     new TransitionResult<MySymbol>(s1, MySymbol.B,     Direction.RIGHT));
s1.transitions.put(MySymbol.BLANK, new TransitionResult<MySymbol>(s2, MySymbol.BLANK, Direction.LEFT));
s2.transitions.put(MySymbol.B,     new TransitionResult<MySymbol>(s3, MySymbol.BLANK, Direction.LEFT));
s3.transitions.put(MySymbol.A,     new TransitionResult<MySymbol>(s3, MySymbol.A,     Direction.LEFT));
s3.transitions.put(MySymbol.B,     new TransitionResult<MySymbol>(s3, MySymbol.B,     Direction.LEFT));
s3.transitions.put(MySymbol.BLANK, new TransitionResult<MySymbol>(s0, MySymbol.BLANK, Direction.RIGHT));

Now, we simply invoke the simulate function on this structure, allowing the user to specify the initial input on the command line in args[0]:

<<main method>>=
public static void main(String[] args) {
    initialize example turing machine
    if (args.length < 1) {
        System.err.println("Syntax: java TuringSimulator <input string>");
        System.exit(-1);
    }
    List<MySymbol> input = MySymbol.parseString(args[0]);
    TuringSimulator<MySymbol> sim = new TuringSimulator<MySymbol>(machine, input);
    sim.run();
}

Now we can see, for example:

<<example_output.txt>>=
$ java TuringSimulator ab
                 v
          start: ab###########################################################
                  v
     scan_right: #b###########################################################
                   v
     scan_right: #b###########################################################
                  v
        reverse: #b###########################################################
                 v
      scan_left: #############################################################
                  v
          start: #############################################################
                   v
          check: #############################################################
                    v
         finish: #############################################################

See Turing machine simulator (Ruby)/Example output for a longer example output.

Download code

Retrieved from "http://literateprograms.org/Turing_machine_simulator_%28Java%29"

Categories: Turing machine simulators | Programming language:Java | Environment:Portable