Turing machine simulator (Ruby)

From LiteratePrograms

We describe a simple Ruby program for simulating an abstract Turing machine. This demonstrates that Ruby is Turing-complete (with the caveat that limitations in word size limit the effective addressable memory).

Formal problem description and assumptions

We define a single-tape Turing machine as a 6-tuple 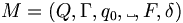$M=(Q, \Gamma, q_0, \textvisiblespace, F, \delta)$ , where

$Q$ is a finite set of states;
$Γ$ is the finite tape alphabet (the symbols that can occur on the tape);
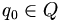$q_0 \in Q$ is the initial state;
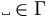$\textvisiblespace \in \Gamma$ is the blank symbol;
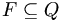$F \subseteq Q$ is the set of accepting (final) states;
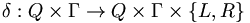$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ is the transition function which determines the action performed at each step.

Initially the tape has the input string on it, followed by an infinite number of blank symbols ( $\textvisiblespace$ ), and the head is at the left end of the tape. At each step we use the transition function to determine the next state, the symbol written on the tape just prior to moving, and the direction to move the head, left (L) or right (R). If we ever reach a final state, the machine halts.

Main simulator

State representation

We represent states and symbols using Ruby symbols. The State class has instance variables describing the tape contents, the current position of the head on the tape, and the current control state. There are methods to initialize, update, and trace the state and convenience methods for accessing the tape:

<<State class>>=
class State
  attr_reader :tape
  attr_reader :head
  attr_reader :control_state
  initialize state method
  update state method
  trace state method
  convenience methods
end

To initialize the state, we initialize the tape with the input string, position the head at the start of the tape, and set the initial control state:

<<initialize state method>>=
def initialize(initial_state, input_string)
  @tape = input_string.dup
  @head = 0
  @control_state = initial_state
end

We can update the state based on what the transition function tells us to do. It supplies a new control state, a symbol to write, and a direction in which to move the head:

<<update state method>>=
def update(next_state, dir, write_symbol)
  raise "Crash!" if next_state == :invalid
  @control_state = next_state
  @tape[@head] = write_symbol
  case dir
  when :left
    raise "Crash!" if @head <= 0
    @head -= 1
  when :right
    @head += 1
  end
end

Note that the head is prevented from moving off the left end. The right end of the tape is auto-expanded with blank symbols by our use of the Array default value above.

For diagnostic purposes, it's also useful to print out some of the details of the state. We'll display the first 60 symbols of tape so that it may easily fit in a terminal. We need to provide a mapping to translate the symbols on the tape to simple screen characters:

<<trace state method>>=
def trace(map)
  if @head < 60
    puts " " * (@head + 17) + "v"
  else
    puts
  end
  tape = (0..60).collect{ |i| map[tape_at(i)] }.join
  puts "%15s: %s" % [ @control_state, tape ]
end

Finally, we provide a convenience methods to fetch symbols from the tape. The tape_at method abstracts access to the tape so we see a blank symbol anywhere the tape has not been written to. The current_symbol method gives us the symbol currently under the head.

<<convenience methods>>=
def tape_at(pos)
  @tape[pos] || :blank
end
def current_symbol
  tape_at(@head)
end

Machine representation

As mentioned above, $Q$ and $Γ$ are represented by Ruby symbols. We also assume the convention, demonstrated above, of using the symbol :blank to represent the blank symbol. The TuringMachine class represents the remaining information about the machine:

<<Turing machine class>>=
class TuringMachine
  attr_accessor :start_state
  attr_reader :accepting_states
  attr_reader :transitions
  initialize machine method
  run simulation method
end

The transition table is a hash which maps state/symbol pairs as the input key which to state/symbol/direction triples as the output value.

While accepting_state is simply initialized to an empty array, we must provide a default value for transitions in order to handle bad input. We use a special state :invalid to indicate this default production. Further specification of the machine is delayed until "programming", discussed below.

<<initialize machine method>>=
def initialize
  @accepting_states = []
  @transitions = Hash.new{ [ :invalid, :blank, :left ] }
end

Simulation

We now come to our primary simulation function. Using our machine state functionality, we can take a programmed TuringMachine object, feed it an input string and step through successive states. We provide a mapping of symbols to characters so that it can be passed on to the state tracing method:

<<run simulation method>>=
def simulate(input_string, map)
  state = State.new(@start_state, input_string)
  state.trace(map)
  until @accepting_states.include?(state.control_state)
    next_state, write_symbol, dir =
      @transitions[[state.control_state, state.current_symbol]]
    begin
      state.update(next_state, dir, write_symbol)
    rescue Exception => e
      puts e
      return
    end
    state.trace(map)
  end
end

Files

We place each of the classes above into their own files, as is the usual ruby idiom. The TuringMachine class depends on the State class, so we require the state library file in the Turing machine library:

<<state.rb>>=
State class
<<turing_machine.rb>>=
require 'state'
Turing machine class

Test driver

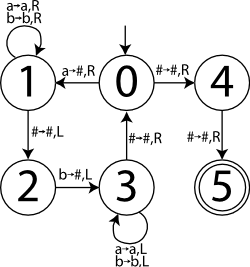
A simple Turing machine recognizing the language aⁿbⁿ

To test the simulation, we'll implement the simple Turing machine shown to the right, which is based roughly on this Turing machine example. This diagram is a state graph, meaning that each vertex represents a state in the machine's finite control, and each edge indicates the input character that must be read to follow that edge, the character to write over it, and the direction to move the head. The initial state is 0 and the only accepting state is 5. It recognizes the following context-free but nonregular language:

$\{{a^n}{b^n} : n \in \mathbb{N}, n \geq 1\}$

The pumping lemma says that this is nonregular, but a Turing machine to recognize it is fairly straightforward. We'll begin by instantiating a TuringMachine object for it and "programming" that object with the start and finish states:

<<Example turing machine>>=
machine = TuringMachine.new
machine.start_state = :start
machine.accepting_states << :finish
define transitions

We then add entries for each arc in the diagram:

<<define transitions>>=
machine.transitions[[ :start,      :a     ]] = [ :scan_right, :blank, :right ]
machine.transitions[[ :scan_right, :a     ]] = [ :scan_right, :a,     :right ]
machine.transitions[[ :scan_right, :b     ]] = [ :scan_right, :b,     :right ]
machine.transitions[[ :scan_right, :blank ]] = [ :reverse,    :blank, :left  ]
machine.transitions[[ :reverse,    :b     ]] = [ :scan_left,  :blank, :left  ]
machine.transitions[[ :scan_left,  :a     ]] = [ :scan_left,  :a,     :left  ]
machine.transitions[[ :scan_left,  :b     ]] = [ :scan_left,  :b,     :left  ]
machine.transitions[[ :scan_left,  :blank ]] = [ :start,      :blank, :right ]
machine.transitions[[ :start,      :blank ]] = [ :check,      :blank, :right ]
machine.transitions[[ :check,      :blank ]] = [ :finish,     :blank, :right ]

Now, we simply invoke the simulate method object, allowing the user to specify the initial input on the command line:

<<example_turing_machine.rb>>=
require 'turing_machine'
unless ARGV.size == 1
  STDERR.puts "Usage: simulate_turing_machine <input string>"
  exit(-1)
end
# convert string into list of symbols
input_string = ARGV.first.split(//).map{ |ch| ch.intern }
Example turing machine
# define trace map
map = {
  :blank => '#',
  :a     => 'a',
  :b     => 'b'
}
# run simulation
machine.simulate(input_string, map)

If we run the program on a string in the language, like "aaabbb", the program will return quickly; otherwise it will work for a bit, then print out "Crash!" when it tries to perform an invalid transition. We ensure it's going through the right intermediate states through the tracing we added to the simulate function.

Now we can see, for example:

<<example_output.txt>>=
$ ruby example_turing_machine.rb ab
                 v
          start: ab###########################################################
                  v
     scan_right: #b###########################################################
                   v
     scan_right: #b###########################################################
                  v
        reverse: #b###########################################################
                 v
      scan_left: #############################################################
                  v
          start: #############################################################
                   v
          check: #############################################################
                    v
         finish: #############################################################

See Turing machine simulator (Ruby)/Example output for a longer example output.

Download code

Retrieved from "http://literateprograms.org/Turing_machine_simulator_%28Ruby%29"

Categories: Turing machine simulators | Programming language:Ruby | Environment:Portable