Turing machine simulator (Haskell)

From LiteratePrograms

This program simulates a Turing machine in Haskell.

<<TuringMachine.hs>>=
module TuringMachine where
import
defineModel
defineInitialState
createModel
runSimulation

Formal problem description and assumptions

We define a single-tape Turing machine as a 6-tuple 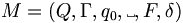$M=(Q, \Gamma, q_0, \textvisiblespace, F, \delta)$ , where

$Q$ is a finite set of states;
$Γ$ is the finite tape alphabet (the symbols that can occur on the tape);
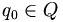$q_0 \in Q$ is the initial state;
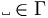$\textvisiblespace \in \Gamma$ is the blank symbol;
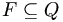$F \subseteq Q$ is the set of accepting (final) states;
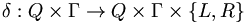$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ is the transition function which determines the action performed at each step.

Initially the tape has the input string on it, followed by an infinite number of blank symbols ( $\textvisiblespace$ ), and the head is at the left end of the tape. At each step we use the transition function to determine the next state, the symbol written on the tape just prior to moving, and the direction to move the head, left (L) or right (R). If we ever reach a final state, the machine halts.

Model Definition

The model uses symbol 0 as the blank symbol and state 0 as the initial state. If the halting action is defined then final states are defined by transitions of the form $( * , * , H A L T)$ . Otherwise the set of final states is empty. Two containers are used in the model:

a List for the tape
a Map for the transition function

<<import>>=
import qualified Data.Map as Map
import Data.Map

A machine's states, symbols and tape are represented using Haskell's built-in arbitrary precision Integer data type since any alphabet and set of states can be mapped to the set of integers. The four base types State, Symbol, Action and Tape are used to define the Turing machine and the Time type is used for defining time steps.

<<defineModel>>=
type State = Integer
type Symbol = Integer
data Action = LEFT | RIGHT | HALT deriving (Enum)
type Tape = [Symbol]
type Time = Integer

The actual machine is represented using two data structures:

a map defining the transition function between a (state, symbol) pair and a (state, symbol, action) triple.
a triple of the form (tape, position, state register) defining the machine's current state.

To uniquely identify each Turing machine a machine id is used of the form (enumeration, number of states, number of symbols).

<<defineModel>>=
type TransitionFunction = Map (State, Symbol) (State, Symbol, Action)
type MachineState = (Tape, Int, State)
data TuringMachine = TuringMachine{
  delta :: TransitionFunction,
  machinestate :: MachineState
}
type MachineID = (Integer, Integer, Integer)

Initial State

The entry point to the simulation defines the machine's initial state. Here are some interesting values to test:

6,3 $(a n)(b n)$ : (2314198519646101975610052599567, 6, 3) *enable halting action
3,2 Busy Beaver: (29452887,3, 2) *enable halting action
2,3 UTM: (596440, 2, 3) *disable halting action
Haskell compiler: ... ;)

<<defineInitialState>>=
main::IO()
main = runSimulation machine numsteps
        where 
                initialtape = replicate 11 0
                initialpos = 5
                initialstate = 0
                machinenumber = 29452887
                numstates = 3
                numsymbols = 2
                numsteps = 16
                halting = True
                machine = createTM (machinenumber, numstates,numsymbols) halting
                            (initialtape, initialpos, initialstate)

Model Creation

First a Turing machine is created from its unique enumeration where the halting action may or may not be defined. The transition function for a Turing Machine is created by modding the machine's enumeration by the total number of possible transitions:

number of possible transitions = (number of states) * (number of symbols) * (number of actions)
transition value = enumeration%(number of possible transitions)

This gives a transition value for iteration (numstates-1,0). The enumeration value for successive transitions up to (0, numsymbols-1) is defined by subtracting the previous transition value from the previous enumeration and dividing by the number of possible transitions:

next enumeration =  ( (previous enumeration) - (previous transition value) ) / (number of possible transitions)

To get a (state, symbol, action) triple, the transition value is applied to the mod-sub-div algorithm using the number of actions then the number of symbols when modding.

<<createModel>>=
createTM::MachineID->Bool->MachineState->TuringMachine
createTM machineid halting initialmachinestate = 
          TuringMachine{
                delta =  createTMDelta machineid halting,
                machinestate = initialmachinestate
           }
createTMDelta::MachineID->Bool->TransitionFunction
createTMDelta (enum,nstates,nsymbols) halting = _createTMDelta (enum,nstates,nsymbols) (if halting then 3 else 2) (nstates-1,0) Map.empty
_createTMDelta::MachineID->Integer->(Integer,Integer)->TransitionFunction->TransitionFunction
_createTMDelta _ _ (-1,_) delta = delta
_createTMDelta (enumeration, numstates, numsymbols) numactions (state, symbol) delta =                        
                          _createTMDelta (enumeration `div` numtriples, numstates, numsymbols) numactions
                             (state- (symbol+1) `div` numsymbols, (symbol + 1) `mod` numsymbols)
                             (Map.insert (state, symbol) (getTransition (enumeration `mod` numtriples) numsymbols numactions) delta)
                        where 
                          numtriples = numstates*numsymbols*numactions
-- convert transition value to (state, symbol, action) triple                      
getTransition::Integer->Integer->Integer->(State, Symbol, Action)
getTransition transition numsymbols numactions = 
                        (tmpval `div` numsymbols, tmpval `mod` numsymbols, toEnum(fromIntegral (transition `mod` numactions))::Action)
                        where tmpval = transition `div` numactions

Simulation

For each step of the simulation the machine's state is printed followed by a transition application. If the number of steps is negative then the simulation executes indefinitely.

<<runSimulation>>=
runSimulation::TuringMachine->Time->IO()
-- end simulation if HALT state is reached
runSimulation (TuringMachine _ (_, _, -1)) _ = putStrLn "HALT"
-- end simulation when time is finished
runSimulation _ 0 = putStrLn "Done"
-- print the current tape, simulate one transition then continue
runSimulation (TuringMachine a (tape, position, register)) t = do
                -- print current state          
                putStrLn (replicate position ' ' ++ "V")
                putStrLn (concatMap show tape ++" q"++ show register)
                runSimulation (simulate (TuringMachine a (tape, position, register)) 1) (t-1)
simulate::TuringMachine->Time->TuringMachine
-- if time is finished then stop simulation
simulate tmachine 0 = tmachine
-- if state register is negative then HALT
simulate (TuringMachine delta (tape, position, -1)) t = TuringMachine delta (tape, position, -1)
-- take one step and continue simulation
simulate tmachine t = 
        simulate (updateState (performAction (writeSymbol (readSymbol tmachine)))) (t-1)

To apply a transition:

1. read the symbol at the tape head's current position then get a transition value of the form (state, symbol, action)

<<runSimulation>>=
readSymbol::TuringMachine->(TuringMachine, (State, Symbol, Action))
readSymbol (TuringMachine delta (tape, position, state)) 
                = (TuringMachine delta (tape, position, state), delta!(state, tape!!position))

2. write the transition symbol to the tape head's current position

<<runSimulation>>=
writeSymbol::(TuringMachine, (State, Symbol, Action))->(TuringMachine, (State, Action))
writeSymbol (TuringMachine a (tape, position, b), (c, newsymbol, d))
                = (TuringMachine a (newtape, position, b), (c, d))
                  where newtape = take position tape ++ [newsymbol] ++ drop (position+1) tape

3. move the tape head to the left, right or halt depending on the transition action and expand the tape if necessary

<<runSimulation>>=
performAction::(TuringMachine, (State, Action))->(TuringMachine, State)
performAction (tmachine, (_, HALT)) = (tmachine, -1)
performAction (TuringMachine a (tape, position, c), (d, LEFT)) = 
                        (TuringMachine a (newtape, newposition, c), d)
                        where newposition = max 0 (position - 1)
                              newtape =  if position == 0 
                                         then [0] ++ tape
                                         else tape
performAction (TuringMachine a (tape, position, c), (d, RIGHT)) = 
                        (TuringMachine a (newtape, newposition, c), d)
                        where newposition = position + 1 
                              newtape = if length tape == position + 1
                                        then  tape ++ [0]
                                        else  tape

4. update the state register with the transition state

<<runSimulation>>=
updateState::(TuringMachine, State)->TuringMachine
updateState (TuringMachine delta (tape, position, _), state) = TuringMachine delta (tape, position, state)

Output

The following output is from running the 3,2 Busy Beaver (29452887,3, 2) with this simulator:

     V
00000000000 q0
      V
00000100000 q1
     V
00000110000 q0
    V
00000110000 q2
   V
00001110000 q1
  V
00011110000 q0
   V
00111110000 q1
    V
00111110000 q1
     V
00111110000 q1
      V
00111110000 q1
       V
00111110000 q1
      V
00111111000 q0
     V
00111111000 q2
HALT

Download code

Retrieved from "http://literateprograms.org/Turing_machine_simulator_%28Haskell%29"