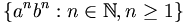Turing machine simulator (OCaml)

From LiteratePrograms

We describe a simple OCaml program for simulating an abstract Turing machine. This demonstrates that OCaml is Turing-complete (with the caveat that limitations in word size limit the effective addressable memory).

Formal problem description and assumptions

We define a single-tape Turing machine as a 6-tuple 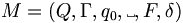$M=(Q, \Gamma, q_0, \textvisiblespace, F, \delta)$ , where

$Q$ is a finite set of states;
$Γ$ is the finite tape alphabet (the symbols that can occur on the tape);
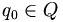$q_0 \in Q$ is the initial state;
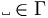$\textvisiblespace \in \Gamma$ is the blank symbol;
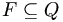$F \subseteq Q$ is the set of accepting (final) states;
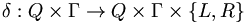$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ is the transition function which determines the action performed at each step.

Initially the tape has the input string on it, followed by an infinite number of blank symbols ( $\textvisiblespace$ ), and the head is at the left end of the tape. At each step we use the transition function to determine the next state, the symbol written on the tape just prior to moving, and the direction to move the head, left (L) or right (R). If we ever reach a final state, the machine halts.

Main simulator

State representation

We will represent the tape by a list of OCaml characters. States are represented by an OCaml option type -- normal states are associated with Some value, while None marks the invalid state. Directions will be represented with an algebraic data type that is either Left or Right

<<types>>=
type dir = Left | Right

Simulation

The main function of our simulator is simulate which performs a single execution step. The first three parameters represent the current execution state, the remainder describes the Turing machine and remains constant throughout the calculation. simulate shall return true if the machine halts on an accepting state and false if it reaches an invalid state.

<<simulator>>=
let rec simulate tape state head_position transition_func accepting_states blank_symbol =
  trace current state;
  act according to current state

In a single simulation step, we have three possible cases depending on the current state value:

<<act according to current state>>=
match state with
 | machine in invalid state
 | machine in accepting state
 | machine running

In invalid state, the machine stops and returns false.

<<machine in invalid state>>=
None -> false

Likewise, if the current state is in the set of accepting states, we stop and return true.

<<machine in accepting state>>=
Some s when List.mem s accepting_states -> true

As long as we're neither in invalid or accepting state, we read the symbol at the current tape position and call the transition function to determine new state, the symbol to write to the tape, and the head move direction:

<<machine running>>=
Some s ->
 let symbol = read symbol at current head position in
 let newstate, newsymbol, movedir = transition_func s symbol in
 next simulation step

To read a symbol from the tape, we define a small utility function that takes a few special cases into account.

<<utility functions>>=
let symbol_at tape position blank_symbol =
  if position < 0 then
    failwith "Invalid tape position"
  else if position >= List.length tape then
    blank_symbol
  else
    List.nth tape position

With its help, reading the current symbol from the tape is straightforward:

<<read symbol at current head position>>=
symbol_at tape head_position blank_symbol

For the next simulation step, we call simulate recursively with an updated tape and head position.

<<next simulation step>>=
simulate (update tape)
         newstate
         (determine new head position)
         transition_func
         accepting_states
         blank_symbol

The head position is updated according to the symbol in movedir.

<<determine new head position>>=
match movedir with
 | Left -> pred head_position
 | Right -> succ head_position

Before the next step, we write the symbol returned by the transition function to the old head position.

<<update tape>>=
write_to_tape tape head_position newsymbol

This is done by another utility function write_to_tape we define as follows:

<<utility functions2>>=
let write_to_tape tape position symbol =
  let l = List.length tape in
  if position < 0 || position > l then
    failwith "Invalid tape position"
  else if position = l then
    tape @ [symbol]
  else
    replace symbol on tape

If the symbol is in the middle of the tape, we copy the tape up to the current position and append the new symbol and the rest of the tape.

<<replace symbol on tape>>=
replace_symbol tape position symbol
<<utility functions>>=
let replace_symbol tape position symbol =
  let rec replace_helper (x::xs) n acc =
    if n = 0 then
      List.rev acc @ symbol :: xs
    else
      replace_helper xs (pred n) (x :: acc)
  in
  replace_helper tape position []

Tracing State

For diagnostic purposes, it's also useful to print out some of the details of a state. We only show the first trace_tape_chars characters of the tape:

<<constants>>=
let trace_tape_chars = 78
<<trace current state>>=
trace_state tape head_position blank_symbol
<<utility functions2>>=
let trace_state tape head_position blank_symbol =
  let print_n_times s n =
    for i = 1 to n do
      print_char s
    done in
  let rec print_tape tape n =
    match tape, n with
       _, 0
     | [], _ -> ()
     | x :: xs, _ -> print_char x;
                     print_tape xs (pred n)
    in
  if head_position < trace_tape_chars then begin
    print_n_times ' ' head_position;
    print_endline "v"
  end;
  print_tape tape trace_tape_chars;
  print_n_times blank_symbol (max 0 (trace_tape_chars - List.length tape));
  print_newline ()

Files

Finally, we put it all together into a source file:

<<simulate_turing_machine.ml>>=
types
constants
utility functions
utility functions2
simulator

This completes the simulator implementation.

Test driver

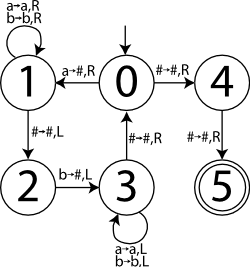
A simple Turing machine recognizing the language aⁿbⁿ

To test the simulation, we'll implement the simple Turing machine shown to the right, which is based roughly on this Turing machine example. This diagram is a state graph, meaning that each vertex represents a state in the machine's finite control, and each edge indicates the input character that must be read to follow that edge, the character to write over it, and the direction to move the head. The initial state is 0 and the only accepting state is 5. It recognizes the following context-free but nonregular language:

$\{{a^n}{b^n} : n \in \mathbb{N}, n \geq 1\}$

The pumping lemma says that this is nonregular, but a Turing machine to recognize it is fairly straightforward. The main task is to transform the state graph into a transition function. We could code such a function for each program we run on the simulator, but a much better idea is to write a generic function which reads the appropriate return values from a data table.

To keep it simple, we use a Hashtbl that maps an input to its corresponding output values. For inputs that do not match any entry in the table, the invalid state is returned.

<<utility functions>>=
let find_trans_state states state symbol blank_symbol =
  try
    let state, symbol, dir = Hashtbl.find states (state, symbol) in
    Some state, symbol, dir
  with Not_found ->
    None, blank_symbol, Left

Now we're ready to define our aⁿbⁿ test. We pick # for the blank symbol.

<<test_driver.ml>>=
open Simulate_turing_machine;;
let test_states = Hashtbl.create 10;;
Hashtbl.add test_states (0,'#') (4,'#',Right);;
Hashtbl.add test_states (0,'a') (1,'#',Right);;
Hashtbl.add test_states (4,'#') (5,'#',Right);;
Hashtbl.add test_states (1,'a') (1,'a',Right);;
Hashtbl.add test_states (1,'b') (1,'b',Right);;
Hashtbl.add test_states (1,'#') (2,'#',Left);;
Hashtbl.add test_states (2,'b') (3,'#',Left);;
Hashtbl.add test_states (3,'a') (3,'a',Left);;
Hashtbl.add test_states (3,'b') (3,'b',Left);;
Hashtbl.add test_states (3,'#') (0,'#',Right);;
let test_anbn_trans_func state symbol =
  find_trans_state test_states state symbol '#'
let anbn_test initial_tape =
  simulate initial_tape (Some 0) 0 test_anbn_trans_func [5] '#';;
anbn_test ['a'; 'b'];;

Now we can see, for example:

v
ab############################################################################
 v
#b############################################################################
  v
#b############################################################################
 v
#b############################################################################
v
##############################################################################
 v
##############################################################################
  v
##############################################################################
   v
##############################################################################

See Turing machine simulator (Scheme)/Example output for a longer example output.

Download code

Retrieved from "http://literateprograms.org/Turing_machine_simulator_%28OCaml%29"

Categories: Turing machine simulators | Programming language:OCaml | Environment:Portable