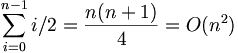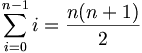Insertion sort (Ruby)

From LiteratePrograms

Jump to: navigation, search
Other implementations: ACL2 | C | C, simple | Eiffel | Erlang | Forth | Haskell | Io | Java | Lisp | OCaml | Python | Python, arrays | Ruby | Scala, list | Smalltalk | Standard ML | Visual Basic .NET

This is a simple example of the insertion sort sorting algorithm, written in Ruby. Since this implementation is intended to be as simple and easy to understand as possible, rather than particularly useful in practice, we will focus on sorting a simple Array of Integers of a given length.

Main algorithm

When sorting an array with insertion sort, we conceptually separate it into two parts:

  • The list of elements already inserted, which is always in sorted order and is found at the beginning of the array;
  • The list of elements we have yet to insert, following.

In outline, our primary function looks like this: 

<<insertion_sort>>=
# Sort an array of integers
def insertion_sort(a)
  a.each_with_index do |el,i|
    insert el into sorted sublist
  end
end

Here, the index i represents both the index of the next element to insert and the length of the sorted sublist constructed so far.

To insert each element, we need to create a hole in the array at the place where the element belongs, then place the element in that hole. We can combine the creation of the hole with the searching for the place by starting at the end and shifting each element up by one until we find the place where the element belongs: 

<<insert el into sorted sublist>>=
# Insert el into the sorted sublist
j = i - 1
while j >= 0
  break if a[j] <= el
  a[j + 1] = a[j]
  j -= 1
end
a[j + 1] = el

On average, we move about half the elements of the already-sorted sublist to insert each element. Consequently, the total number of assignments on average to sort n elements is:

\sum_{i=0}^{n-1} i/2 = \frac{n(n+1)}{4} = O(n^2)

In the worst case, the list is in reverse sorted order, so that each element must push up all other elements encountered so far. The total number of assignments in this case is twice the average case:

\sum_{i=0}^{n-1} i = \frac{n(n+1)}{2}

Test driver

To try out the sort, we can write a simple test driver file with the following structure: 

<<insertion_sort.rb>>=
insertion_sort
helper functions
test main

Our test main will create a small array, sort it, then print out the result: 

<<test main>>=
a = [ 5, 1, 9, 3, 2 ]
insertion_sort(a)
print out a
check that the array is sorted

Checking that the array is sorted is a pretty simple loop but we have to make sure that we handle the cases where there are zero or one elements in the array, hence we start at the second element and always compare an element to the one before it. 

<<helper functions>>=
def checkThatArrayIsSorted(array)
  1.upto(array.size - 1) do |i|
    if array[i-1] > array[i]
      puts "The array is not in sorted order at position #{i-1}"
    end
  end
end
<<check that the array is sorted>>=
checkThatArrayIsSorted(a)

A better test main might ask for numbers from the user or generate an array of random numbers. For sanity's sake, we will print out the array so that we can visually verify it is sorted. To print the array, we join the elements with newlines ("\n"). 

<<print out a>>=
puts a.join("\n")

This completes our simple exposition of iterative insertion sort in Ruby. On UNIX with Ruby installed, you can run this sample by typing "ruby insertion_sort.rb".

Download code
Retrieved from "http://literateprograms.org/Insertion_sort_%28Ruby%29"
Views