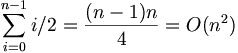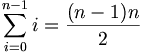Insertion sort (Java)

From LiteratePrograms

Insertion sort or "bin sort" is a simple but inefficient sorting algorithm that repeatedly takes the next element and inserts it in its correct position in the sorted list constructed so far. This article describes some implementations of insertion sort written in Java.

Integer arrays

For simplicity we begin with sorting integer arrays. When sorting an array with insertion sort, we conceptually separate it into two parts:

The list of elements already inserted, which is always in sorted order and is found at the beginning of the array;
The list of elements we have yet to insert, following.

In outline, our primary method looks like this:

<<integer array insertion sort>>=
public static void insertionSort(int[] a) {
    for (int i=1; i < a.length; i++) {
        insert a[i] into sorted sublist
    }
}

Here, the index i represents both the index of the next element to insert and the length of the sorted sublist constructed so far.

To insert each element, we need to create a hole in the array at the place where the element belongs, then place the element in that hole. We can combine the creation of the hole with the searching for the place by starting at the end and shifting each element up by one until we find the place where the element belongs. This overwrites the element we're inserting, so we have to save it in a variable first:

<<insert a[i] into sorted sublist>>=
/* Insert a[i] into the sorted sublist */
int v = a[i];
int j;
for (j = i - 1; j >= 0; j--) {
    if (a[j] <= v) break;
    a[j + 1] = a[j];
}
a[j + 1] = v;

On average, we move about half the elements of the already-sorted sublist to insert each element. Consequently, the total number of assignments on average to sort n elements is:

$\sum_{i=0}^{n-1} i/2 = \frac{(n-1)n}{4} = O(n^2)$

The summation starts from zero because the maximum number of assignments is one less than the serial number of the element in the array.

In the worst case, the list is in reverse sorted order, so that each element must push up all other elements encountered so far. The total number of assignments in this case is twice the average case:

$\sum_{i=0}^{n-1} i = \frac{(n-1)n}{2}$

Object arrays

The simplest way to generalize the algorithm is what the Java API does, by writing it to sort arrays of Objects. The Java API supplies two methods:

Arrays.sort(Object[] a): Sorts an array of objects implementing Comparable, which provides a "natural" ordering.
By just changing the element type to Object and the "<" to a call to compareTo, we can implement a sort with the same interface as this call:

<<object array insertion sort>>=
public static void insertionSort(Object[] a) {
    for (int i=0; i < a.length; i++) {
        /* Insert a[i] into the sorted sublist */
        Object v = a[i];
        int j;
        for (j = i - 1; j >= 0; j--) {
            if (((Comparable)a[j]).compareTo(v) <= 0) break;
            a[j + 1] = a[j];
        }
        a[j + 1] = v;
    }
}

Arrays.sort(Object[] a, Comparator c): Sorts an array of objects using the given comparator. Removed in Java 1.5 in favor of a generic implementation.<p>Implementing a method with this interface is as simple as adding an argument and using its compare() method in place of the compareTo method used above:

<<object array insertion sort with comparator>>=
public static void insertionSort(Object[] a, Comparator c) {
    for (int i=0; i < a.length; i++) {
        /* Insert a[i] into the sorted sublist */
        Object v = a[i];
        int j;
        for (j = i - 1; j >= 0; j--) {
            if (c.compare(a[j], v) <= 0) break;
            a[j + 1] = a[j];
        }
        a[j + 1] = v;
    }
}
<<import statements>>=
import java.util.Comparator;

Generic interface

In Java 1.5 we can use a generic interface that provides stronger type checking and better performance for primitive types. We wish to restrict our element type so that it can be compared, which we can do using T extends Comparable. However, in Java 1.5, Comparable itself takes a generic parameter specifying the type of object that it compares. The most obvious obvious choice is to use T:

<T extends Comparable<T>>

However, suppose that T is Dog, and rather than extend Comparable<Dog>, it extends the more general Comparable<Animal>, where Animal is a superclass of Dog. In this case it can still be compared to any other Dog object, so this should not prevent us from sorting a list of dogs. We express this in Java 1.5 by replacing T with the constraint "? super T", meaning "any superclass of T":

<T extends Comparable<? super T>>

Inserting this, and replacing Object with T in the first object-based implementation, we get the following:

<<generic array insertion sort>>=
public static <T extends Comparable<? super T>>
void insertionSortGeneric(T[] a) {
    for (int i=1; i < a.length; i++) {
        /* Insert a[i] into the sorted sublist */
        T v = a[i];
        int j;
        for (j = i - 1; j >= 0; j--) {
            if (a[j].compareTo(v) <= 0) break;
            a[j + 1] = a[j];
        }
        a[j + 1] = v;
    }
}

A second generic implementation is like the second object-based implementation, using an explicit comparator:

<<generic array insertion sort with comparator>>=
public static <T>
void insertionSortGeneric(T[] a, Comparator<? super T> c) {
    for (int i=1; i < a.length; i++) {
        /* Insert a[i] into the sorted sublist */
        T v = a[i];
        int j;
        for (j = i - 1; j >= 0; j--) {
            if (c.compare(a[j], v) <= 0) break;
            a[j + 1] = a[j];
        }
        a[j + 1] = v;
    }
}

Here, the generic type signature means that the comparator is able to compare objects of the element type or any superclass of the element type. This is the same interface used by the new generic sort function in Java 1.5.

Test code

We can test the implementation by simply generating a random array of a specified size, sorting it, and then testing that it is ordered. Here's some simple test code that does this for the first, simple integer array sort implementation:

<<test main>>=
public static void main(String[] args) {
    int size = Integer.parseInt(args[0]);
    Random rand = new Random();
    int[] a = new int[size];
    for(int i=1; i<size; i++) {
        a[i] = rand.nextInt(size);
    }
    insertionSort(a);
    for(int i=1; i<size; i++) {
        if (a[i] < a[i-1]) {
            System.out.println("ERROR");
        }
    }
}
<<import statements>>=
import java.util.Random;

Files

Finally, we place the static methods in a class for reuse. We create two versions of the class, one for Java 1.4 and earlier and one for Java 1.5:

<<InsertionSort14.java>>=
import statements
class InsertionSort14 {
    integer array insertion sort
    object array insertion sort
    object array insertion sort with comparator
    test main
}

<<InsertionSort15.java>>=
import statements
class InsertionSort15 {
    integer array insertion sort
    object array insertion sort
    object array insertion sort with comparator
    generic array insertion sort
    generic array insertion sort with comparator
    test main
}

Download code

Retrieved from "http://literateprograms.org/Insertion_sort_%28Java%29"

Categories: Programming language:Java | Environment:Platform independent | Insertion sort